Previously I wrote a bit about Junos’ $9 ‘hashes’ (they’re actually reversibly encrypted passwords). While considering the ramifications of nearly-cleartext credentials stored in config files, I thought about the $1 hashes used to authenticate users via telnet, HTTP, console, HTTPS, and SSH (don’t use the first two). I’ve been told multiple times that the “system login user authentication encrypted-password” statements, usually at the beginning of a config, can be copied around as desired to grant that user access. This is similar in function to an SSH public key, but that line of thinking is dangerous – while properly-sized RSA public keys can’t realistically factored to their original private keys, some password hashes can be.
$1 hashes are from md5crypt(). md5crypt was written in 1995 and added to FreeBSD version 2 shortly after. It’s a few extra operations on top of what is essentially 1000 rounds of md5 (stretching) operating on the password and an 8-byte salt. It outputs a base64-encoded version of a 32-byte md5 hash. Apple’s well-commented code from OS X is a good way to see exactly how it works. The output format is $s separating the format, salt, and hash:
$1$SSSSSSSS$hhhhhhhhhhhhhhhhhhhhhh
(id) (salt) (hash)
MD5 is extremely fast, which means it’s extremely broken as a password hash algorithm. My desktop’s fairly new mid-end GPU (a GTX 960) can do 7.1 billion MD5 hashes/second. md5crypt’s stretch factor of 1000 (plus a bit more with the overhead of the extra operations) is still very cooperative to cracking – my GTX 960 does 2.6 million hashes/sec, roughly 2700x slower than MD5 but all things considered very, very fast for password hashing. I won’t write too much about hashing algorithms and speed, as it’s been covered extremely thoroughly by many people. Bottom line: use as slow of an algorithm as is reasonable, with a variable work factor. This leaves bcrypt, scrypt, and PBKDF2. This article and its 2007 predecessor are excellent primers on password hashing, salts, and rainbow tables.
Back to md5crypt – 2.6 million hashes/sec on commodity hardware is very fast. Poul-Henning Kamp, the original author of md5crypt(), wrote in 2012 that md5crypt is now “as prone to brute-force attacks as the DES based UNIX crypt was back in 1995: Any 8 character password can be found in a couple of days.” That’s damning, but how about some numbers?
I’m using oclHashcat, specifically cudahashcat64.exe, and their mask syntax is useful to describe keyspaces:
?l = a-z
?u = A-Z
?d = 0-9
?s = «space»!"#$%&'()*+,-./:;<=>?@[\]^_`{|}~
?a = ?l?u?d?s
Here are a few password search spaces along with the time it’d take my GTX960 to run through the entire space using md5crypt:
?a x 7 : 308915776 (308 million) – 3 x 10^8 : 2 minutes
?a x 8 : 69833729609375 (69 billion) – 6.9 x 10^13 : 310 days
?l?u?d x 8 : 218340105584896 (218 trillion) – 2.1 x 10^14 : 972 days
?a x 8 : 6634204312890625 (6 quadrillion) – 6.6 x 10^15 : 80.86 years
?l x 10 : 141167095653376 (141 trillion) – 1.4 x 10^14 : 628 days
?l?u x 10 : 2779905883635712 (2 quadrillion) – 2.7 x 10^15 : 33.88 years
?l?u?d x 10 : 13537086546263552 (13 quadrillion) – 1.3 x 10^16 : 165 years
?a x 10 : 47720649502202481 (47 quadrillion) – 4.7 x 10^16 : 581 years
?a x 12 : 190107953018704786 (190 quadrillion) – 1.9 x 10^17 : 2317 years
I assume there’s some mismatch in the symbol sets, because the search space numbers from Hashcat don’t quite match up with the GRC Haystack. I’ve duplicated a bit of effort from the Haystack, but its three estimated cracking speeds don’t quite cover md5crypt on commodity hardware, and it’s fun to get numbers that are relevant to the subject at hand.
You can see that the times escalate extremely quickly, and that as you get past 10 characters it becomes unfeasible. Remember, though, that these times are for my single $300 GPU – a well-resourced entity (be it corporate, state, or criminal) that could afford hundreds or thousands of GTX 960s changes the playing field greatly. Using napkin math, a farm of 3000 GTX 960s retailing for $900k could now break a 10-length ?l?u password in 4 days.
Also remember that the times listed above are to exhaust the entire search space. Hashcat outputs a somewhat sequential ordering of the search space, so if my password is ‘Andrew15’ it’ll be found much sooner than ‘Rachel99’ (assuming a pure bruteforce with no strategic masking). Humans aren’t random and neither are their passwords, but if they were, the average discovery would occur 50% of the way through the search space.
What does this look like in practice? First, we get a password hash straight out of Junos:
tylerkerr@srx210# set system login user test authentication plain-text-password
New password:
Retype new password:
[edit]
tylerkerr@srx210# show | compare
[edit system login]
+ user test {
+ authentication {
+ encrypted-password "$1$6Ub0uM5t$08QKpPT1ZO0GjwcVe6mTP1"; ## SECRET-DATA
OK, our hash is $1$6Ub0uM5t$08QKpPT1ZO0GjwcVe6mTP1. Let’s take it to Hashcat.
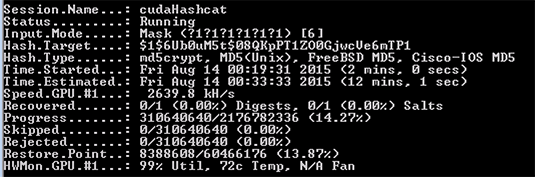
To keep the demo short, let’s say that I’m going to try the correct search space – ?l?u x 6. The Hashcat syntax is (on Windows):
cudahashcat64.exe -m500 -a3 $1$6Ub0uM5t$08QKpPT1ZO0GjwcVe6mTP1 -1 ?l?d ?1?1?1?1?1?1
-m500 is hash type 500 – see Hashcat’s impressive list of supported hashes here
-a3 is attack type 3, mask attack, which is just a tunable bruteforce
-1 defines a custom mask variable, which in this case is ?l?d, and six ?1s sets our search space at 6 chars. It’s possible to automatically increment if you’ve chosen or know the character set but not the password length.
This is what it looks like:
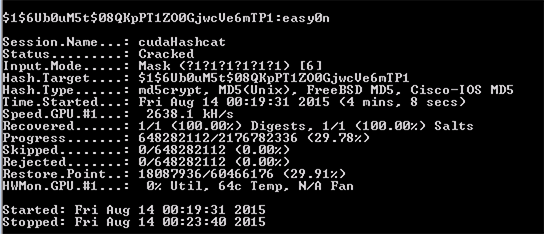
And on completion:
The password was “easy0n” (“easy0ne” would’ve taken longer than I wanted). 4:05 of real time, from an estimated 12 minutes.
Out of curiosity, I asked a colleague to try the same operation on his Titan X, a $1000 single-GPU card:
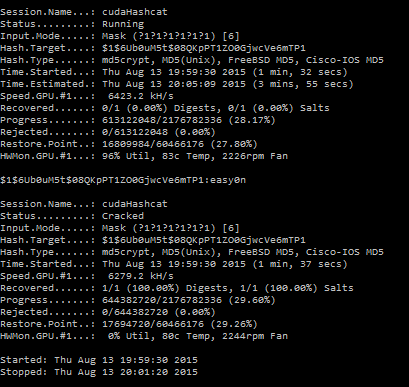
Done in 1:37, around 2.5x faster.
So what does this mean regarding Junos’ $1 hashes? Even though it’s an old algorithm, good passwords are hard enough to crack that coworkers with access to your config files probably aren’t going to be able to crack them. Even a determined attacker that somehow obtains your hash would still need to devote significant resources to cracking it (again, as long as you used a reasonable password).
All of that said, it’s still concerning that these are even realistically breakable at all. A state or multinational entity would be able to break even very good passwords hashes with md5crypt – it’s an old algorithm. Cisco has already started moving to both scrypt and PBKDF2. $1 hashes should probably be treated as secret data, which, to their credit, Juniper appends as a comment to all $1 hashes and $9 passwords. Now, Next time: what happens when you use set system login password format sha1?
emad
2018-07-31 — 02:59
hi
i have the following password in my cfg file could you please give me its decryption
$1$D6mt6GZX$labm5GNkzFEUc/vMwBxo.0
best regards
matt
2023-06-05 — 12:49
You mention that your hardware can search:
?a x 7 : 308915776 (308 million) – 3 x 10^8 : 2 minutes
?a x 8 : 69833729609375 (69 billion) – 6.9 x 10^13 : 310 days
I’m not sure how those things add up when you state you are using ” ?l?d” and your screenshot shows about 14 minutes to get through x6 key space.
?a is far larger, and x7 is way larger than that, yet it only takes 2 minutes? My hardware does 4475 kH/s and would take 180 days to get through ?a x 7.